|
关注:1
2013-05-23 12:21
求翻译:Given this database of local geometry, learning a Gaus- sian model of φi(x) is straightforward. Assume that the user has specified m input curves, each consisting of k nodes x (j) i ,i = 1..k, j = 1..m. We compute a dc-dimensional mean µ (φ) i and a dc ×dc covariance matrix Σ(φ) i of the sets {dx(j) i }j for each node i是什么意思?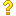 待解决 待解决
 悬赏分:1
- 离问题结束还有 悬赏分:1
- 离问题结束还有
Given this database of local geometry, learning a Gaus- sian model of φi(x) is straightforward. Assume that the user has specified m input curves, each consisting of k nodes x (j) i ,i = 1..k, j = 1..m. We compute a dc-dimensional mean µ (φ) i and a dc ×dc covariance matrix Σ(φ) i of the sets {dx(j) i }j for each node i
问题补充: |
|
2013-05-23 12:21:38
定本地几何此数据库,学习φI的高斯模型(x)是简单的。
|
|
2013-05-23 12:23:18
给出地方几何这个数据库,学会φi Gaus-西安模型(x)是直接的。假设,用户有specifi编辑m输入曲线,每个包括的k结x (j)我, i = 1.k, j = 1.m。我们计算一dc尺寸卑鄙µ (φ) i和dc ×dc协方差矩阵Σ (集合{dx (j)我}每个结的j的φ) i我=横跨曲线的1.k使用PCA。
|
|
2013-05-23 12:24:58
正在翻译,请等待...
|
|
2013-05-23 12:26:38
给出了此数据库学习 φi(x) 高斯模型简单的局部几何。假设该用户具有进行 m 输入的曲线,每个组成的 k 节点 x (j) 我,我 = 1..k,j = 1..m。我们计算直流三维平均 µ (φ),第一和一个直流 × 直流协方差矩阵 Σ(φ) 我集 {dx(j) 我} 为每个节点 j 我 = 1..k 两端使用 PCA 的曲线。所以愈合子的车流量方差通常会维比原始的描述符空间因为他们是从只有很少一部分计算和前 sumably 高度相关的例子要低得多。我们将存储这些统计学来表征训练集。
|
|
2013-05-23 12:28:18
正在翻译,请等待...
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区